Llevo muchos años haciéndolo mal, lo reconozco, ha sido por puro desconocimiento: no sabía lo que tenía que saber. ¿Qué paradoja, verdad?
Resulta que herramientas tan cotidianas como Excel ya nos permiten desde siempre hacer análisis de correlación entre datos, pero lo que viene por defecto instalado ahí es la correlación de Pearson, uno de los métodos más famosillos que se conoce.
Pues vaya por delante que el desconocimiento no nos exime de responsabilidad y me debía a mi misma este artículo, una vez que ya me hago cargo de lo que hay que saber cuándo se puede usar ese método de correlación y por qué es importante para el rigor de nuestros análisis.
Vamos con el artículo pues.
¿Para qué necesitamos la correlación como SEOs?
Con la cantidad de datos que manejamos en nuestro día a día analizando a partir de herramientas como Google Analytics, Google Search Console o herramientas de terceros (Semrush, Ahrefs, Sistrix, etc.), podemos hacer uso de la correlación para tratar de entender la relación entre variables y que nos ayude a identificar patrones que puedan hablarnos de comportamientos.
Si somos capaces de entender este tipo de relaciones tendremos un mayor entendimiento y eso nos lleva al conocimiento más profundo de lo que estamos analizando y por ende, a definir mejores hipótesis, trazar mejores estrategias y dar con las tácticas oportunas.
Con el análisis de correlación también estamos capacitados para descubrir como se distribuyen los datos y si estos presentan datos extremos o también conocidos como «outliers». En ocasiones, tener valores que están muy alejados (por el lado inferior o el superior) nos puede ensuciar o distorsionar el análisis tremendamente. Y ya se sabe, en un mundo como el SEO que ya de por si tiene muchísimo ruido, nuestra oportunidad es intentar minimizar las posibles confusiones que estén en nuestra mano.
¿Qué métodos más habituales tenemos a nuestra disposición y qué requisitos estadísticos se deben s cumplir para usar uno u otro?
Tanto si has estudiado estadística básica en el Instituto como si has usado la fórmula de CORRELACIÓN que viene en Excel instalada, hay dos métodos que son archiconocidos o hiperusados: Pearson y Spearman.
Correlación Pearson
Tenemos al querido método Pearson, que es un poco más exquisito, así que para poder usarlo necesitas que tus datos cumplan una serie de requisitos:
- Lo primero, las variables han de ser numéricas (y que no haya datos vacíos)
- Lo segundo es que entre las variables que estudias ha de existir una relación lineal
- Lo tercero es que los datos deben cumplir una distribución normal
¿Cómo interpretamos el dato que nos da Pearson? Fácil e intuitivo: valores cercanos a 1 o -1 indican una fuerte relación lineal positiva o negativa (respectivamente).
Pero eh, hay una gran pega además de los 2 requisitos mencionados, si tus datos tienen valores extremos, este método de correlación puede distorsionar muchísimo su cálculo y perder mucha precisión, claro.
Correlación Spearman
Por otro lado está el hippie de Spearman que no requiere distribuciones normales, es menos sensible a datos atípicos y puede trabajar incluso cuando la relación entre las variables no es lineal.
Sin embargo, todo tiene sus desventajas, en su caso, su manía de convertir datos a rangos le hace perder parte de información y si se usa este método en variables con relaciones lineales puras, puede patinar un poquillo.
El único requisito para usar este método de correlación es que haya una tendencia constante en la relación de las variables, creciente o decreciente.
Ejemplo de aplicación de ambos con datos de Google Search Console
Vamos con un ejemplo. Seguramente si comparamos los Clics con el CTR, extraidos de Google Search Console, casi seguro vamos a obtener correlaciónl pues el cálculo del CTR ya incluye a los Clics.
Por tanto, vamos a comparar Impresiones con Clics, para ver qué tipo de relación tienen. Uso datos reales de un proyecto de contenidos de deporte.
Una primera cosa que podemos hacer es un gráfico de dispersión ya vemos como se relacionan ambas variables y también aprovechamos para ver si hay valores extremos, esos puntitos que se separan de la mayoría.
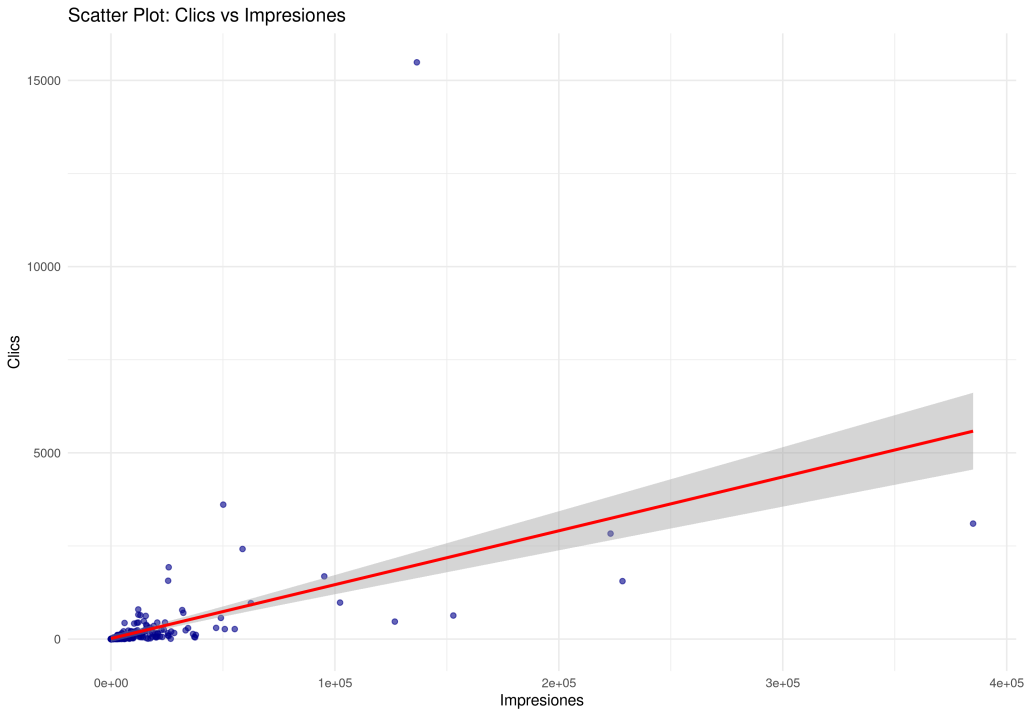
Luego, en un segundo paso, podemos comprobar si los datos cumplen la distribución normal o no, usando el test Shapiro-Wilk. Si usáramos un programa como R para calcularlo, sería una simple línea para cada variable tal que así:
shapiro_clicks <- shapiro.test(seo_data$clicks)
shapiro_impressions <- shapiro.test(seo_data$impressions)
#p-value > 0,05 = si es distribución normal
#p-value < 0,05 = no es distribución normalCon este resultados podríamos confirmar qué método tenemos que usar.
cor_pearson <- cor(seo_data$clicks, seo_data$impressions, method = "pearson")
cor_spearman <- cor(seo_data$clicks, seo_data$impressions, method = "spearman")En mis datos de ejemplo, ya veo que:
- Los datos si presentan relación lineal pero existen outliers
- Los datos no presentan una distribución normal
- Debería utilizar Spearman
Ejemplo de resultados en plan visual y entendible hasta por mi sobrino el pequeño:

PD: esto es una app que tengo yo hecha en R para que me lo ponga todo facilito y entendible
¿Y podemos hacer una matriz de correlación entre todas las variables que tengo?
Esto tiene bastante potencial para entender las relaciones en pares de variables, lo cual nos puede dar pistas de qué combinaciones tienen correlaciones fuertes o débiles, positivas o negativas.
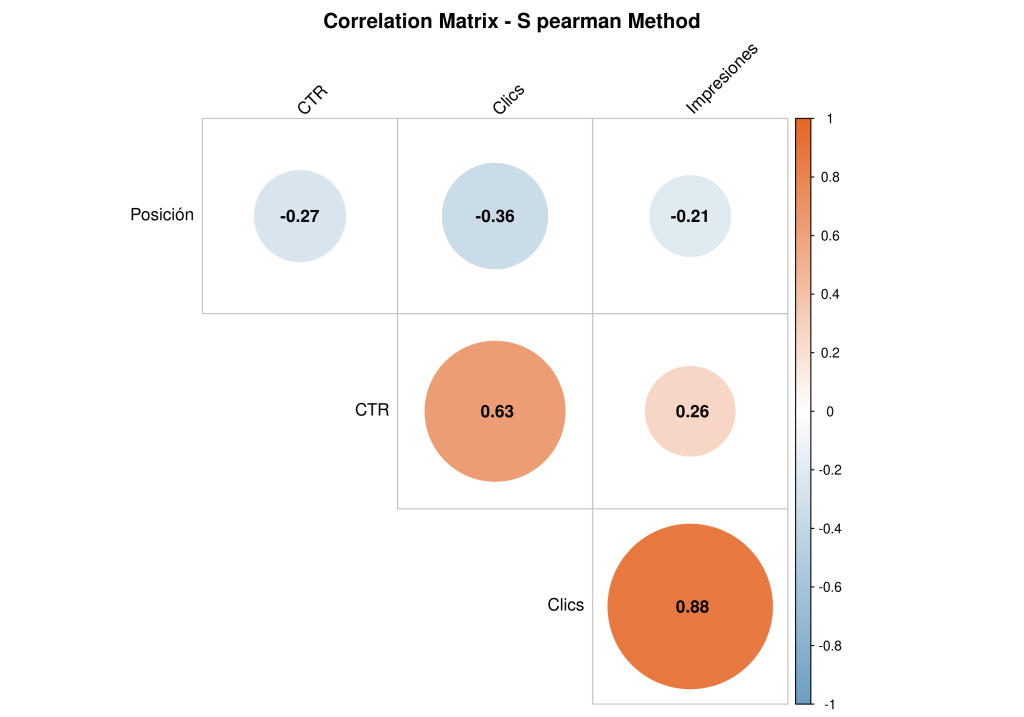
Lo interesante de esto es entender la lógica y funcionamiento de los datos que estamos añadiendo a la mtriz.
La única correlación negativa es la de Posición, ¿por qué? Porque el valor más positivo es menor, el más negativo es mayor. Si quiero posicionar en el mejor ranking, quiero estar en el 1, cuanto más grande es el número, peor es el rendimiento. Entonces…..
La relación entre Posición y Clics es negativa, cuando la posición se hace «más grande», los Clics disminuyen, lógica pura, ¿verdad? Si, pero ahora con rigor estadístico.
Siguiendo con el ejemplo de relacionar Impresiones y Clics, podríamos interpretar así:

PD: si, es otra vez la app que hice en R para tener todo facilito y entendible
¿Y nos vale con cualquier tipo de muestra de datos?
Esto es otro de esos conceptos que no tenemos controlado en nuestro radar de cómo hacer análisis sin sacar un dedo por la ventana. Cuando tengo pocos datos, ¿sigue siendo válido todo esto que contamos? ¿Cuánto de «verdadera» tiene la conclusión que sacamos en muestras más pequeñas o más grandes?
La estadística que tiene siempre una respuesta para todo pues no iba a ser menos en esta ocasión. Mira tu, yo me entero en 2025, pero aquí lo dejo escrito para quien quiera tenerlo en cuenta para lo suyo también.
En R lo podríamos calcular así, considerando unos valores de base para garantizar que haya un efecto mínimo en las relaciones de las variables (0,3), un error asumible pequeño (0,05) y que la potencia (0,8) del modelo haga el resto, o sea, que sea factible detectar esa correlación en altas probabilidades.
# una correlación de r = 0.3 con un nivel de significación de 0.05 y potencia de 0.80.
power_result <- pwr.r.test(r = 0.3, sig.level = 0.05, power = 0.8, alternative = "two.sided")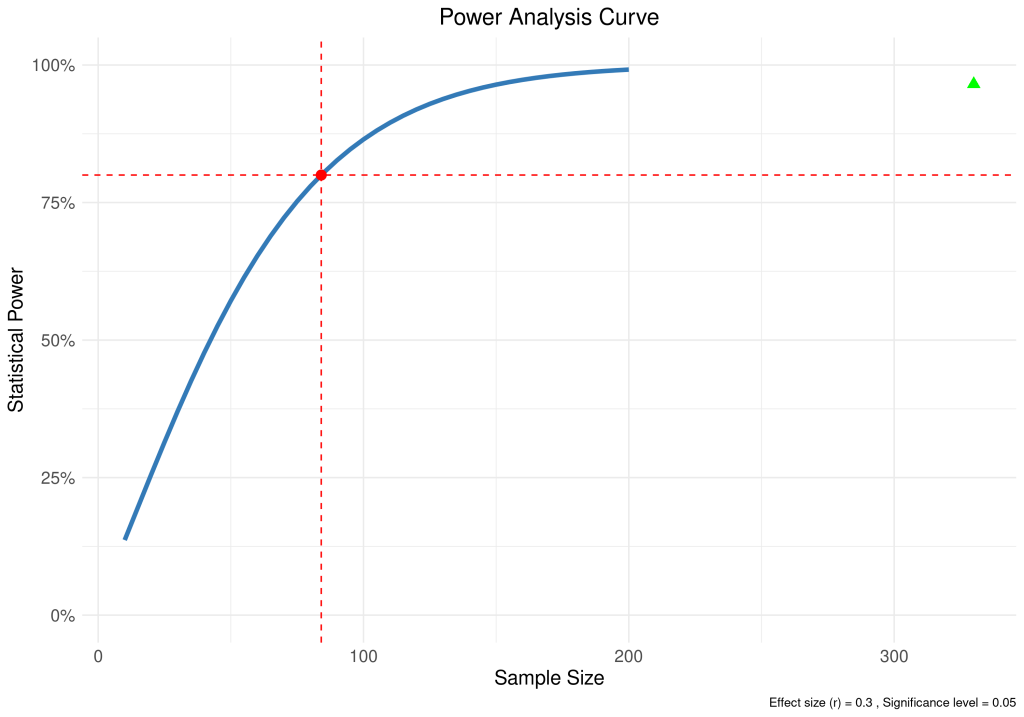
Y esto, explicado bien mascadito, sería algo como esto:

PD: …. hola, soy la app otra vez
Casos de uso probables para analizar en SEO
- Evaluar la relación entre posición y CTR
Teóricamente: cuanto mejor sea la posición (más baja), mayor debería ser el CTR. Si la correlación es baja o no significativa, podría haber otros factores influyendo (ej. snippets, intenciones de búsqueda). - Relación entre impresiones y clics
Téoricamente: más impresiones deberían generar más clics (aunque no siempre). Si no hay correlación fuerte, se podría investigar si la calidad de las búsquedas está afectando. - Análisis de correlación entre backlinks y rankings
Teóricamente: más backlinks deberían mejorar el ranking (disminuir la posición media). Si la correlación es baja, otros factores pueden influir (ej. calidad de los enlaces, contenido, autoridad del dominio). - ¿Más palabras en un artículo mejora el ranking?
Teóricamente: si hay correlación negativa, podría indicar que los contenidos más largos tienden a posicionar mejor. - Impacto de la velocidad de carga en el CTR
Teóricamente: a mayor tiempo de carga, menor CTR. Si la correlación es baja, tal vez hay otros factores (intención de búsqueda, tipo de contenido). - Relación entre cambios en el algoritmo de Google y caídas de tráfico
Teóricamente: si hay una correlación negativa fuerte en las fechas del Update con el descenso de visibilidad o clics. Si la correlación es baja, el sitio puede no haber sido afectado directamente. - ¿Más contenido en una página mejora el tiempo de permanencia?
Teóricamente: si hay correlación positiva enrte wordcount y tiempo en página, puede suponer que más contenido debería aumentar el tiempo en página (o que el contenido resuelve muy bien la intent o es de alta calidad). Si la correlación es baja, puede haber otros factores que no estamos considerando.
Hay muchos más casos de uso de SEO donde aplicar las correlaciones, pero ojo, hay cosas que debemos considerar:
- Falsos positivos y falsos negativos
- Mirar solo pares de variables, dejan fuera otras variables que seguro están entrando en juego
- Cuidado con el sesgo de confirmación
- Correlación no implica causalidad
Resumen y consideraciones finales
Tanto si haces análisis de SEO, como estudios de factores y otras casuísticas más, siempre es un punto a considerar tener controlada la estadística básica que se esconde detrás de la comparación de variables.
Espero que con este post se pueda dar mayor rigor a los análisis y empezar ya teniendo claros los factores que intervienen, de forma sencilla.
Por último, estos métodos no son los únicos que se pueden usar, hay muchísimos más, pero estos son los más comunes y extendidos. También merece la pena mencionar que se pueden hacer Correlaciones Parciales, es decir, añadir variables de confusión para ver qué influencia tiene esa tercera variable respecto de las 2 analizadas. No lo he añadido para ir más al grano e introducir el tema. No descarto desarrollar el tema de correlaciones parciales en otro artículo más adelante, pero eso, que existir, existen.
Por si puede ser de ayuda, dejo un pequeño diagrama de flujo con lo que habría que considerar en base a los datos que tengamos.
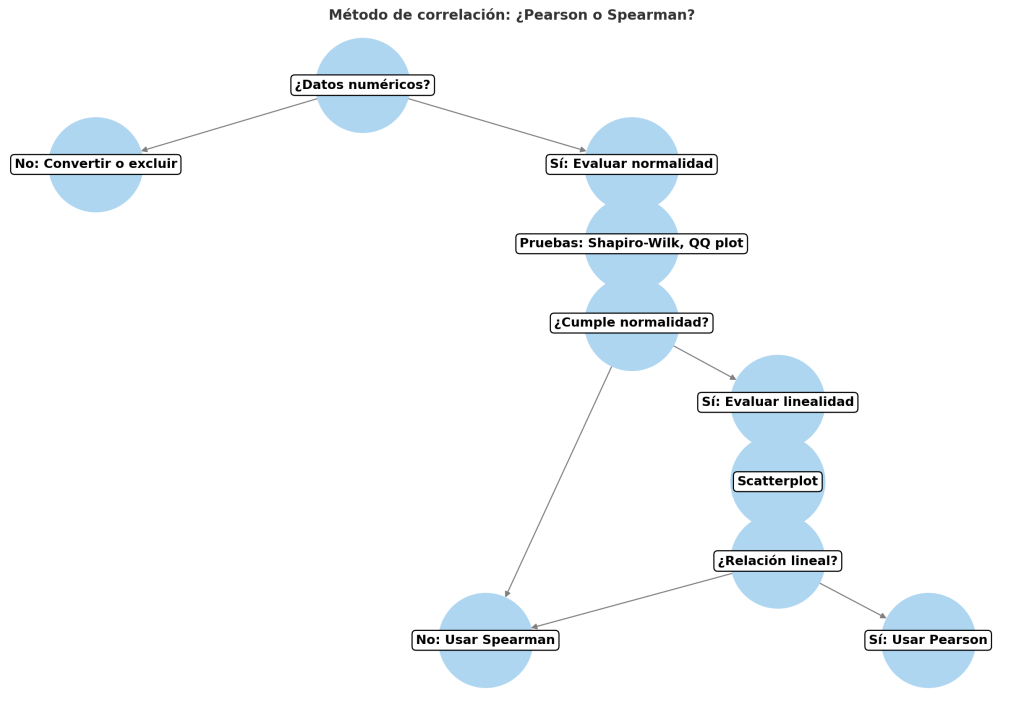
¿Cuánto tiempo me ha llevado?
La idea del post la he extraido de mi máster de ciencia de datos y estadística, así que he aplicado ese concepto a SEO, para poder interiorizarlo mejor y de paso, lo comparto con quien quiera leerlo y aprender junto a mi.
El código mostrado de R, está basado en las clases y Claude me ayudó a mejorarlo y montar la dichosa app
Por lo demás, montar el post lo acabo de hacer en un par de horitas, más o menos, considerando que me voy de viaje corriendo, ¡me ha cundido!
Entre unas cosas y otras, el tiempo ha sido alrededor de 12 horas, mientras escuchaba un grupo nuevo llamado Ultraligera
¡Disfruta el post!
Soy MJ Cachón
Consultora SEO desde 2008, directora de la agencia SEO Laika. Volcada en unir el análisis de datos y el SEO estratégico, con business intelligence usando R, Screaming Frog, SISTRIX, Sitebulb y otras fuentes de datos. Mi filosofía: aprender y compartir.
